Convolution Layers¶
Overview¶
DistDL’s The Distributed Convolutional layers use the distributed primitive
layers to build various distributed versions of PyTorch ConvXd layers.
That is, it implements
where \(*\) is the convolution operator and the tensors \(x\), \(y\), \(w\), and \(b\) are partitioned over a number of workers.
For the purposes of this documentation, we will assume that an arbitrary global input tensor \({x}\) is partitioned by \(P_x\). Another partition \(P_y\), may exist depending on implementation. similarly, the weight tensor \(w\) may also have its own partition is partitioned by \(P_w\). The bias \(b\) is implicitly partitioned depending on the nature of \(P_w\).
Implementation¶
The partitioning of the input and output tensors strongly impacts the necessary operations to perform a distributed convolution. Consequently, DistDL has multiple implementations to satisfy some special cases and the general case.
Public Interface¶
DistDL provides a public interface to the many distributed convolution
implementations that follows the same pattern as other public interfaces, such
as the Linear Layer and keeping in line with
the PyTorch interface. The distdl.nn.conv module provides the
distdl.nn.conv.DistributedConv1d,
distdl.nn.conv.DistributedConv2d, and
distdl.nn.conv.DistributedConv3d types, which through use the class
distdl.nn.conv.DistributedConvSelector to dispatch an appropriate
implementation, based on the structure of \(P_x\), \(P_y\), and
\(P_W\).
Current implementations include those for:
Feature-distributed Convolution¶
The simplest distributed convolution implementation, and the one that generally requires the least workers, has input (and outout) tensors that are distributed in feature-space only. This is also, likely, the most common use-case.
Construction of this layer is driven by the partitioning of the input tensor \(x\), only. Thus, the partition \(P_x\) drives the algorithm design. With a pure feature-space partition, the output partition will have the same structure, so there is no need to specify it. Also, with no partition in the channel dimension, the learnable weight tensor is assumed to be small enough that it can trivially be stored by one worker.
Assumptions¶
The global input tensor \(x\) has shape \(n_{\text{b}} \times n_{c_{\text{in}}} \times n_{D-1} \times \cdots \times n_0\).
The input partition \(P_x\) has shape \(1 \times 1 \times P_{D-1} \times \cdots \times P_0\), where \(P_{d}\) is the number of workers partitioning the \(d^{\text{th}}\) feature dimension of \(x\).
The global output tensor \(y\) will have shape \(n_{\text{b}} \times n_{c_{\text{out}}} \times m_{D-1} \times \cdots \times m_0\). The precise values of \(m_{D-1} \times \cdots \times m_0\) are dependent on the input shape and the kernel parameters.
The output partition \(P_y\) implicitly has the same shape as \(P_x\).
The weight tensor \(w\) will have shape \(n_{c_{\text{out}}} \times n_{c_{\text{in}}} \times k_{D-1} \times \cdots \times k_0\).
The weight partition does not necessarily explicitly exist, but implicitly has shape \(1 \times 1 \times 1 \times \cdots \times 1\).
Any learnable bias is stored on the same worker as the learnable weights.

An example setup for a 1D distributed convolutional layer, where \(P_x\) has shape \(1 \times 1 \times 4\), \(P_y\) has the same shape, and \(P_W\) has shape \(1 \times 1 \times 1\).¶
Forward¶
Under the above assumptions, the forward algorithm is:
Use a Broadcast Layer to broadcast the learnable \(w\) from a single worker in \(P_x\) to all of \(P_x\). If necessary, a different broadcast layer, also from a single worker in \(P_x\) to all of \(P_x\) broadcasts the learnable bias \(b\).
The weight and bias tensors, post broadcast, are used by the local convolution.
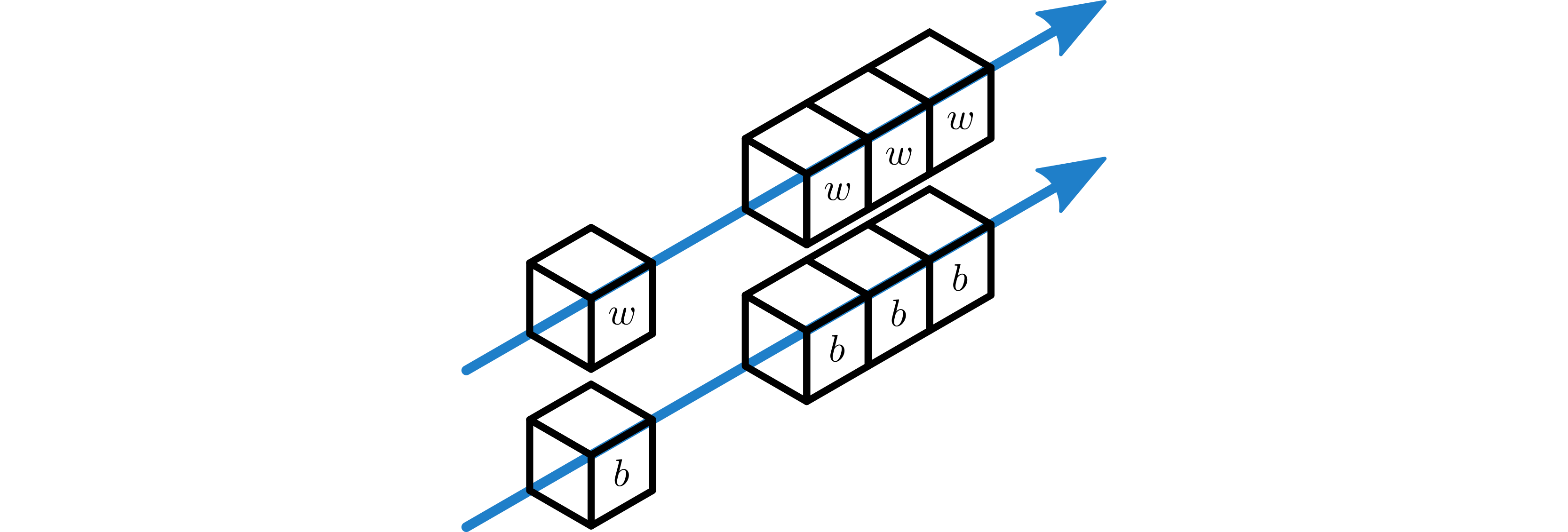
\(w\) and \(b\) are broadcast to all workers in \(P_x\).¶
Perform the halo exchange on the subtensors of \(x\). Here, \(x_j\) must be padded to accept local halo regions (in a potentially unbalanced way) before the halos are exchanged. The output of this operation is \(\hat x_j\).

Subtensors of \(x\), \(x_j\) must be padded to accept the halo data.¶

Forward halos are exchanged on \(P_x\), creating \(\hat x_j\).¶
Perform the local forward convolution application using a PyTorch
ConvXdlayer. The bias is added everywhere, as each workers output will be part of the output tensor.

The \(y_i\) subtensors are computed using native PyTorch layers.¶
The subtensors in the inputs and outputs of DistDL layers should always be able to be reconstructed into precisely the same tensor a sequential application will produce. Because padding is explicitly added to the input tensor to account for the padding specified for the convolution, the output of the local convolution, \(y_i\), should exactly match that of the sequential layer.

Adjoint¶
The adjoint algorithm is not explicitly implemented. PyTorch’s autograd
feature automatically builds the adjoint of the Jacobian of the
feature-distributed convolution forward application. Essentially, the
algorithm is as follows:
The gradient output \(\delta y_i\) is already distributed across its partition, so the adjoint of the Jacobian of the local convolutional layer can be applied to it.

Each worker computes its local contribution to \(\delta w\) and \(\delta x\), given by \(\delta w_j\) and \(\delta x_j\), using PyTorch’s native implementation of the adjoint of the Jacobian of the local sequential convolutional layer. If the bias is required, each worker computes its local contribution to \(\delta b_j\), \(\delta \hat b\) similarly.
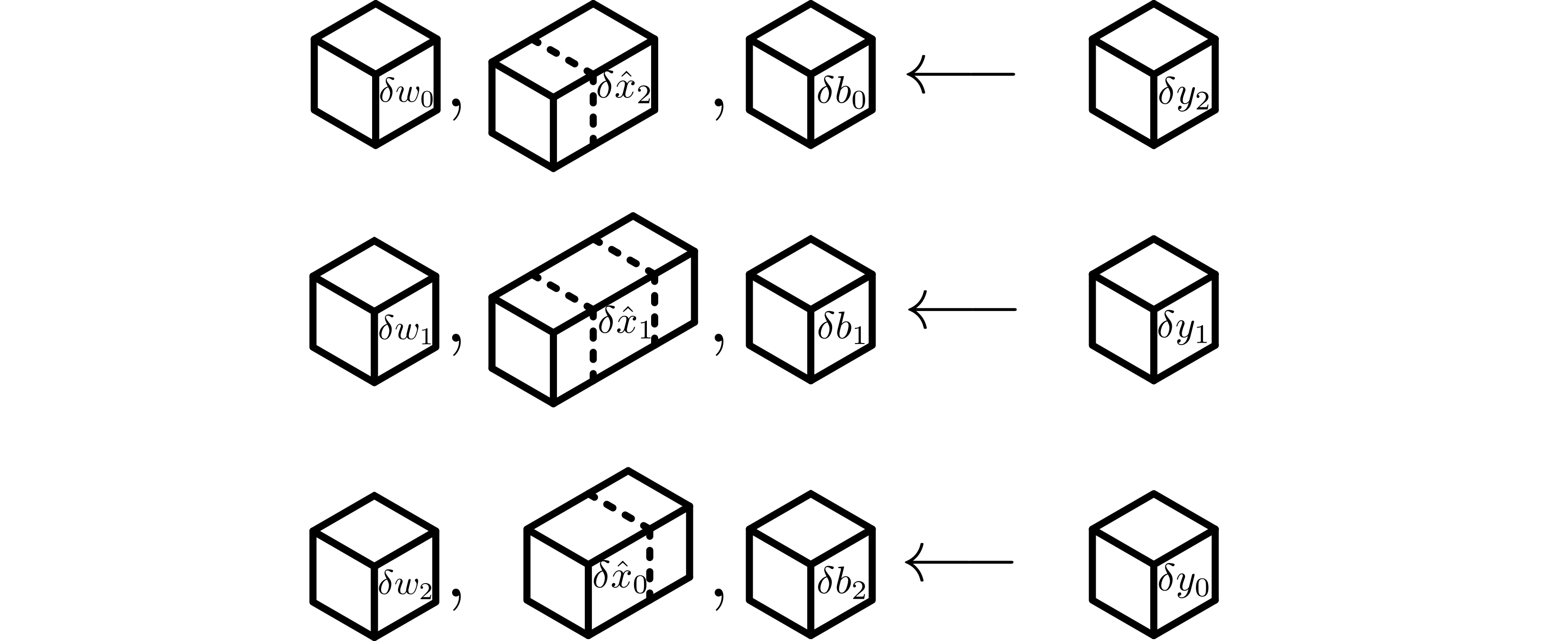
Subtensors of \(\delta w_j\), \(\delta \hat x_j\), and \(\delta b_j\) are computed using native PyTorch layers.¶
The adjoint of the halo exchange is applied to \(\delta \hat x\), which is then unpadded, producing the gradient input \(\delta x\).

Adjoint halos of \(\delta \hat x\) are exchanged on the \(P_x\).¶

Subtensors \(\delta \hat x_j\) must be unpadded to after the halo regions are cleared :to create, creating \(\delta x\).¶
Sum-reduce the partial weight gradients, \(\delta w_j\), to produce the total gradient \(\delta w\) on the relevant worker in \(P_x\).
If required, do the same thing to produce \(\delta b\) from each worker’s \(\delta b_j\).
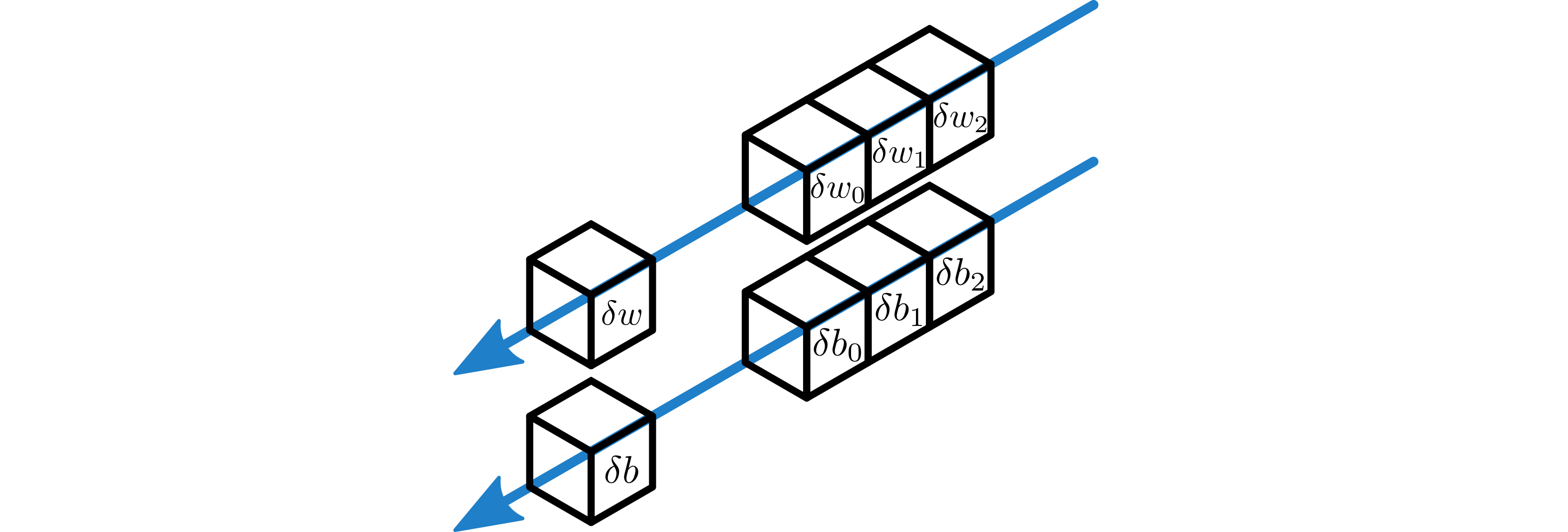
\(\delta w\) and \(\delta b\) are constructed from a sum-reduction on all workers in \(P_x\).¶
Channel-distributed Convolution¶
DistDL provides a distributed convolution layer that supports partitions in the channel-dimension only. This pattern may be useful when layers are narrow in feature space.
For the construction of this layer, we assume that the fundamental unit of work is driven by dense channels in \(w\). Thus, the structure of the partition \(P_w\) drives the design. This layer admits differences between \(P_x\) and \(P_y\), so all three partitions, including \(P_w\), must be specified. It is assumed that there is no partitioning in the feature-space for the input and output tensors.
Assumptions¶
The global input tensor \(x\) has shape \(n_{\text{b}} \times n_{c_{\text{in}}} \times n_{D-1} \times \cdots \times n_0\).
The input partition \(P_x\) has shape \(1 \times P_{c_{\text{in}}} \times 1 \times \cdots \times 1\), where \(P_{c_{\text{in}}}\) is the number of workers partitioning the channel dimension of \(x\).
The global output tensor \(y\) will have shape \(n_{\text{b}} \times n_{c_{\text{out}}} \times m_{D-1} \times \cdots \times m_0\). The precise values of \(m_{D-1} \times \cdots \times m_0\) are dependent on the input shape and the kernel parameters.
The output partition \(P_y\) has shape \(1 \times P_{c_{\text{out}}} \times 1 \times \cdots \times 1\), where \(P_{c_{\text{out}}}\) is the number of workers partitioning the channel dimension of \(y\).
The global weight tensor \(w\) will have shape \(n_{c_{\text{out}}} \times n_{c_{\text{in}}} \times k_{D-1} \times \cdots \times k_0\).
The weight partition, which partitions the entire weight tensor, \(P_w\) has shape \(P_{c_{\text{out}}} \times P_{c_{\text{in}}} \times 1 \times \cdots \times 1\).
The learnable bias, if required, is stored on a \(P_{c_{\text{out}}} \times 1 \times 1 \times \cdots \times 1\) subset of the weight partition.
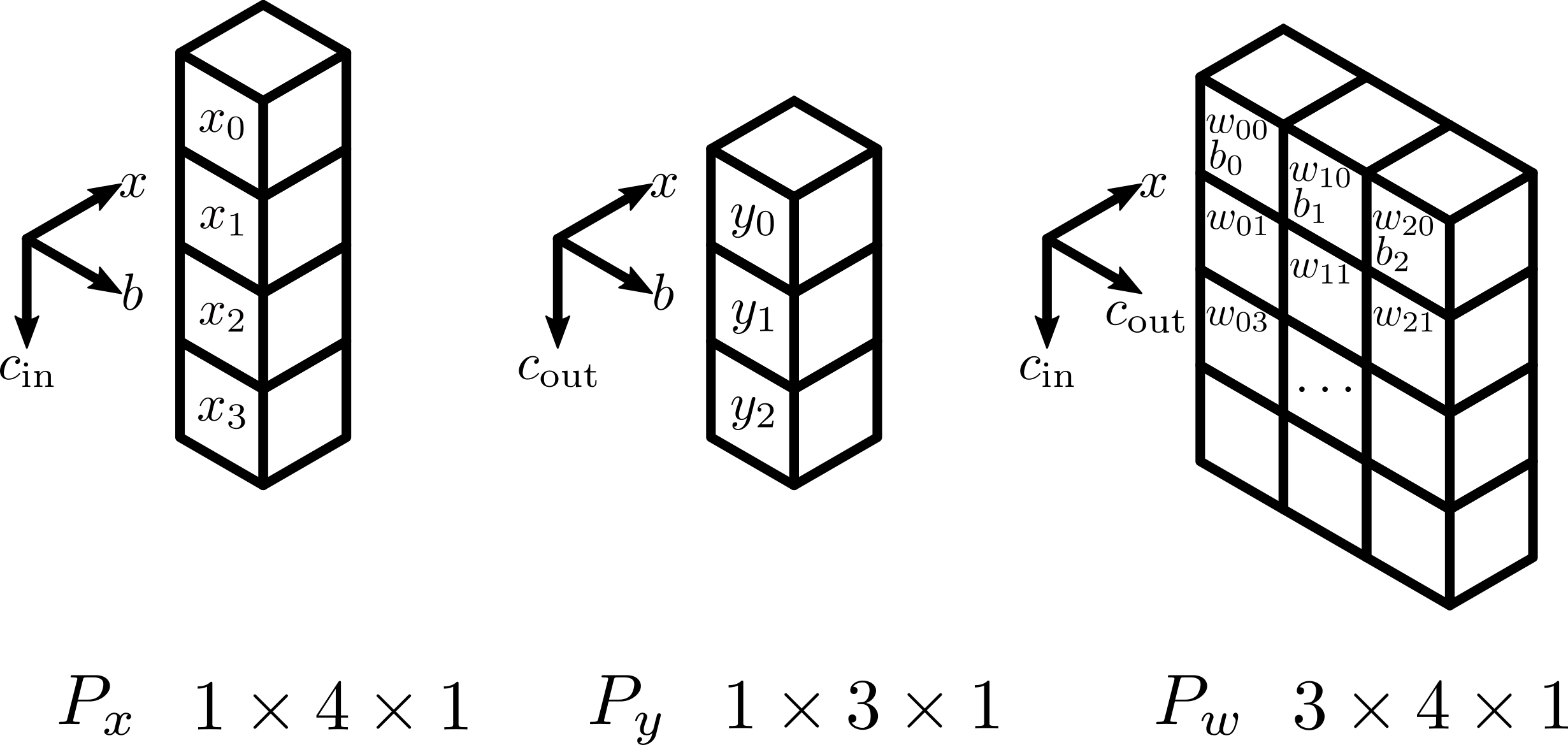
An example setup for a 1, channel distributed convolutional layer, where \(P_x\) has shape \(1 \times 4 \times 1\), \(P_y\) has the shape \(1 \times 3 \times 1\), and \(P_w\) has shape \(3 \times 4 \times 1\).¶
Forward¶
Under the above assumptions, the forward algorithm is:
Use a Broadcast Layer to broadcast subtensors of \(x\) from \(P_x\) along the \(P_{c_{\text{out}}}\) dimension of \(P_w\), creating local copies of \(x_j\).
Perform the local forward convolutional layer application using a PyTorch ConvXd layer. Note that the bias is only added on the specified subset of \(P_w\). Each worker now has a portion of a subtensor, denoted \(y_i\), of the global output vector.
Use a SumReduce Layer to reduce the partial subtensors of \(y\) along the \(P_{c_{\text{in}}}\) dimension of \(P_w\) into \(P_y\). Only one subtensor in each row of \(P_w\) contains the a subtensor of the bias, so the output tensor correctly assimilates the bias.
Adjoint¶
The adjoint algorithm is not explicitly implemented. PyTorch’s autograd
feature automatically builds the adjoint of the Jacobian of the
channel-distributed convolution forward application. Essentially, the
algorithm is as follows:
Broadcast the subtensors of the gradient output, \(\delta y\) from \(P_y\) along the \(P_{c_{\text{in}}}\) dimension of \(P_w\), creating copies \(y_i\).
Each worker in \(P_w\) computes its local subtensor of \(\delta w\) and its contribution to the subtensors of \(\delta x\) using the PyTorch implementation of the adjoint of the Jacobian of the local sequential convolutional layer. If the bias is required, relevant workers compute the local subtensors of \(\delta b\) similarly.
Sum-reduce the partial subtensors of the gradient input, \(\delta x_j\), along the \(P_{c_{\text{out}}}\) dimension of \(P_w\) into \(P_x\).
Generalized Distributed Convolution¶
DistDL provides a distributed convolution layer that supports partitioning in both channel- and feature-dimensions. This pattern is expensive. Each of the previous two algorithms can be derived from this algorithm.
For the construction of this layer, we assume that the fundamental unit of work is driven by dense channels in \(w\). Thus, the structure of the partition \(P_w\) drives the design. This layer admits differences between \(P_x\) and \(P_y\), so all three partitions, including \(P_w\), must be specified. Any non-batch dimension is allowed to be partitioned.
Assumptions¶
The global input tensor \(x\) has shape \(n_{\text{b}} \times n_{c_{\text{in}}} \times n_{D-1} \times \cdots \times n_0\).
The input partition \(P_x\) has shape \(1 \times P_{c_{\text{in}}} \times P_{D-1} \times \cdots \times P_0\), where \(P_{c_{\text{in}}}\) is the number of workers partitioning the channel dimension of \(x\) and \(P_{d}\) is the number of workers partitioning the \(d^{\text{th}}\) feature dimension of \(x\).
The global output tensor \(y\) will have shape \(n_{\text{b}} \times n_{c_{\text{out}}} \times m_{D-1} \times \cdots \times m_0\). The precise values of \(m_{D-1} \times \cdots \times m_0\) are dependent on the input shape and the kernel parameters.
The output partition \(P_y\) has shape \(1 \times P_{c_{\text{out}}} \times P_{D-1} \times \cdots \times P_0\), where \(P_{c_{\text{out}}}\) is the number of workers partitioning the channel dimension of \(y\) and the feature partition is the same as \(P_x\).
The weight tensor \(w\) will have shape \(n_{c_{\text{out}}} \times n_{c_{\text{in}}} \times k_{D-1} \times \cdots \times k_0\).
The weight partition \(P_w\) has shape \(P_{c_{\text{out}}} \times P_{c_{\text{in}}} \times P_{D-1} \times \cdots \times P_0\).
The learneable weights are stored on a \(P_{c_{\text{out}}} \times P_{c_{\text{in}}} \times 1 \times \cdots \times 1\) subset of the weight partition.
Any learnable bias is stored on a \(P_{c_{\text{out}}} \times 1 \times 1 \times \cdots \times 1\) subset of the weight partition.
Forward¶
Under the above assumptions, the forward algorithm is:
Perform the halo exchange on the subtensors of \(x\). Here, \(x_j\) must be padded to accept local halo regions (in a potentially unbalanced way) before the halos are exchanged. The output of this combined operations is \(\hat x_j\).
Use a Broadcast Layer to broadcast the local learnable subtensors of \(w\) along the first two (\(P_{c_{\text{out}}} \times P_{c_{\text{in}}}\)) dimensions of \(P_w\) to all of \(P_w\) (creating copies of \(w_{ij}\)). If necessary, a different broadcast layer broadcasts the local learnable subtensors of \(b\) also from the first dimension (\(P_{c_{\text{out}}}\)) of \(P_w\) to the subset of \(P_w\) which requires it (creating local copies of \(b_i\)).
Use a Broadcast Layer to broadcast \(\hat x\) along the matching dimensions of \(P_w\).
Perform the local forward convolution application using a PyTorch
ConvXdlayer. The bias is added only in the subset of , as each workers output will be part of the output tensor.
Use a SumReduce Layer to reduce the subtensors of \(\hat y\) along the matching dimensions of \(P_w\). Only one subtensor in each reduction dimension contains the a subtensor of the bias, so the output tensor correctly assimilates the bias.
The subtensors in the inputs and outputs of DistDL layers should always be able to be reconstructed into precisely the same tensor a sequential application will produce. Because padding is explicitly added to the input tensor to account for the padding specified for the convolution, the output of the local convolution, \(y_i\), should exactly match that of the sequential layer..
Adjoint¶
The adjoint algorithm is not explicitly implemented. PyTorch’s autograd
feature automatically builds the adjoint of the Jacobian of the
channel-distributed convolution forward application. Essentially, the
algorithm is as follows:
The gradient output \(\delta y_i\) is already distributed across its partition, so the adjoint of the Jacobian of the local convolutional layer can be applied to it.
Broadcast the subtensors of the gradient output, \(\delta y_i\) from \(P_y\) along the matching dimensions of \(P_w\).
Each worker in \(P_w\) computes its local part of \(\delta w_{ij}\) and \(\delta x_j\) using the PyTorch implementation of the adjoint of the Jacobian of the local sequential convolutional layer. If the bias is required, the relevant workers in \(P_w\) also compute their portion of \(\delta b_i\) similarly.
Sum-reduce the local contributions of \(\delta x_j\) along the matching dimensions of \(P_w\) to \(P_x\).
Sum-reduce the local partial weight gradients along the first two (\(P_{c_{\text{out}}} \times P_{c_{\text{in}}}\)) dimensions of \(P_w\), to produce total subtensors of \(\delta w\).
If required, do the same thing to produce local subtensors of \(\delta b\) from each relevant worker’s local subtensor of \(\delta b\).
The adjoint of the halo exchange is applied to \(\delta \hat x_j\), which is then unpadded, producing the gradient input \(\delta x_j\).
Convolution Mixin¶
Some distributed convolution layers require more than their local subtensor to compute the correct local output. This is governed by the “left” and “right” extent of the convolution kernel. As these calculations are the same for all convolutions, they are mixed in to every convolution layer requiring a halo exchange.
Assumptions¶
Convolution kernels are centered.
When a kernel has even size, the left side of the kernel is the shorter side.
Warning
Current calculations of the subtensor index ranges required do not correctly take stride and dilation into account.
